[最も好ましい] 三角 錐 表面積 求め 方 148263
三角錐の体積 =底面積×高さ× (1/3) = ABD×AC× (1/3) =8×3× (1/3) =8㎤ 2.三角錐の表面積の求め方 三角錐の側面は、全て三角形です。 したがって、三角形の面積を求める方法を四か所で行うことで、必然的に三角錐の表面積を求めることができます。 しかし、よほど特殊な数値設定がされない限り、三角錐の表面積を一度に簡単に求めることはできません。 したがって、基本的
三角 錐 表面積 求め 方- この公式は,右図のように三角形を $3$ つに分割して,それぞれの三角形の面積を足すことにより導けます. 逆に,三角形の面積と,$3$ 辺の長さがわかっていると,内接円の半径が求47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ,円柱とその展開図である。 次の問いに答えよ。
三角 錐 表面積 求め 方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
 |  |  |
「三角 錐 表面積 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | ||
「三角 錐 表面積 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「三角 錐 表面積 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「三角 錐 表面積 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「三角 錐 表面積 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「三角 錐 表面積 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  |  |
「三角 錐 表面積 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「三角 錐 表面積 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
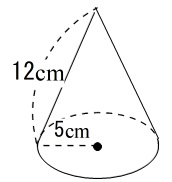
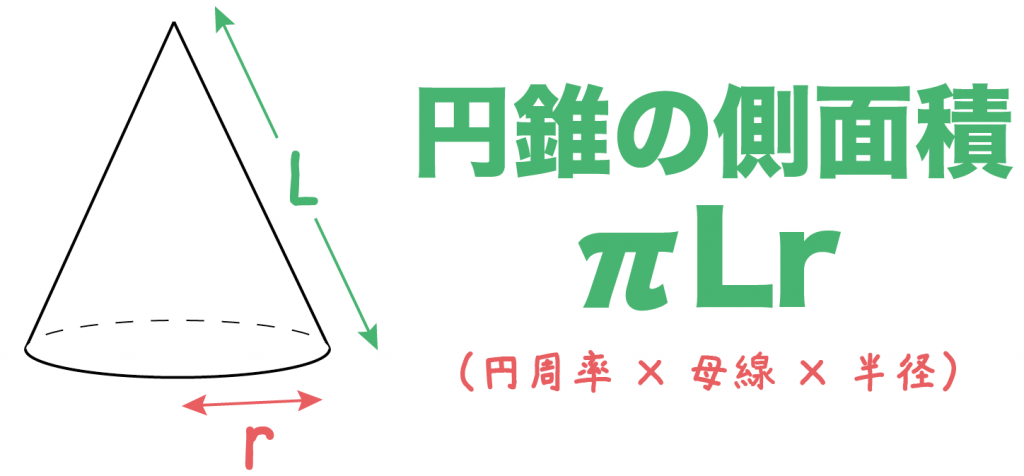
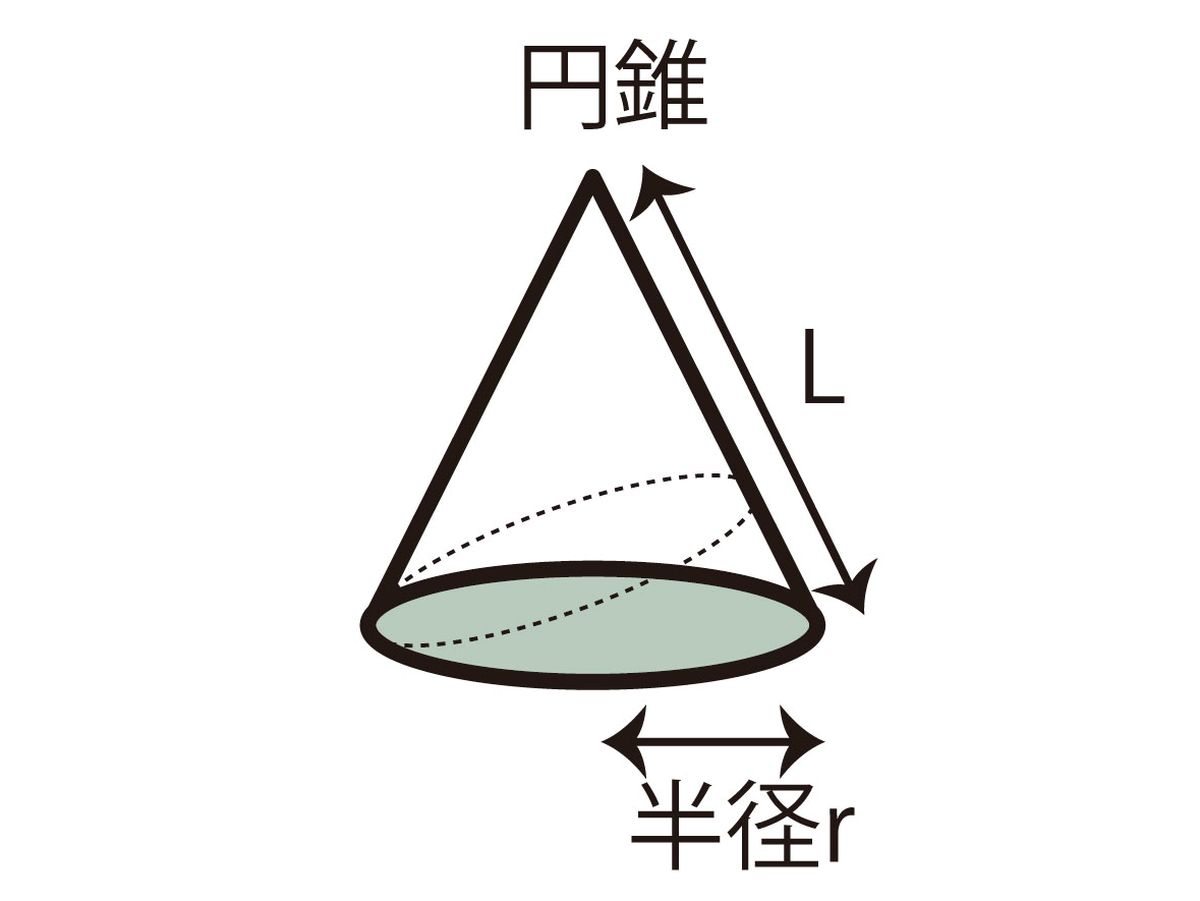
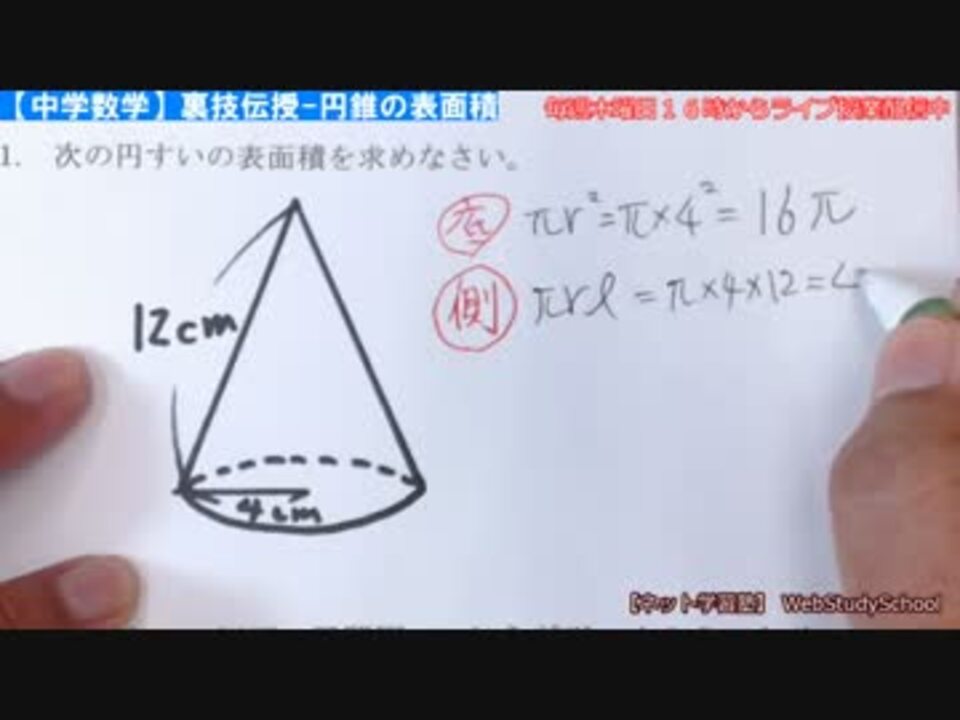
次の図形の体積と表面積を求めよ。 (1)底面が1辺6cmの正方形、側面はすべて合同で底辺が6cm、高さが5cmの三角形の四角錐。 また四角錐の高さは4cmとする。 (2)底面が半径5cm、母線が13cm、高さが12cmの円錐。 (1)『体積=底面積×高さ× 1 3 1 3 』なので、 6 ×6 ×4 × 1 3=48cm3 6 × 6 × 4 × 1 3 = 48 c m 3 側面積は底辺6cm、高さ5cmの三角形が4つの面積をあわせたものなので この三角錐の高さはab=ad=4cm。 cに集まる辺はどれも90゜ですからaはcの真上にきます。 この同じ三角錐を4つ集めると、 底辺が8c㎡で高さ4cmの四角錐になるわけです。ただ、逆に出題される場合もありそうですね。 この三角錐は立方体の頂点と、
コメント
コメントを投稿